A comparison of the displays of the Oculus Quest 2, Rift, and Quest's

In a new YouTube video of Tauriel wood compares pictures of the Oculus Quest, Quest 2 Oculus and Oculus Rift (S).
As in the previous comparison of the Oculus Rift (S) and the Oculus Rift, youtuber takes on a 4K camera through the lenses of the glasses VR. Using different applications, it compares image displays with each other. In addition to the games Elite Dangerous and Assetto Corsa also uses the image of the tests for vision.
Comparison of Quests without the support of 90 Hz
Wood claims that he installed the latest updates for Oculus Quest and Quest 2. Support 90 Hz for Quest 2 was absent. Oculus will be presenting it via a software update later this year. Also need to improve communication with Oculus Link. Oculus has announced the updates Link, the stream on the PC and Move function .
It should be recalled: Oculus Quest 2 is equipped with an LCD RGB display with a resolution of 1920 x 1832 pixels and a refresh rate of currently 72 Hz, in contrast to the Oculus Quest OLED display with a resolution of 1440 x 1600 pixels and 72 Hz. Oculus Rift (S) provides a resolution of 1280 x 1440 pixels and a frame rate of 80 Hz on the LCD display.
Oculus Quest 2: the failure of black level and letters
No wonder OLED display Oculus Quest, it seems, has the advantage in the first comparison of the black level. Although Rift (S) looks a little pale, you can see clearly in bright artifacts in the Quest 2.

This leadership is melting away in comparison when playing Assetto Corsa. If you look at the stall, Rift (S) shows a more pure black and much richer color than Quest. While Rift (S) and especially the Quest output visible mosquito mesh on the image, this effect is clearly better to have Quest 2.

The negative effect of screen Quest even more obvious on a Board with letters and numbers. The numbers on the right edge is almost not visible in the first line, and in the Quest 2 the last line can also be read. Even if black color will again become faded, here Quest 2 still looks better. Rift (S) seems sharper with the letters, but the numbers are very fuzzy.
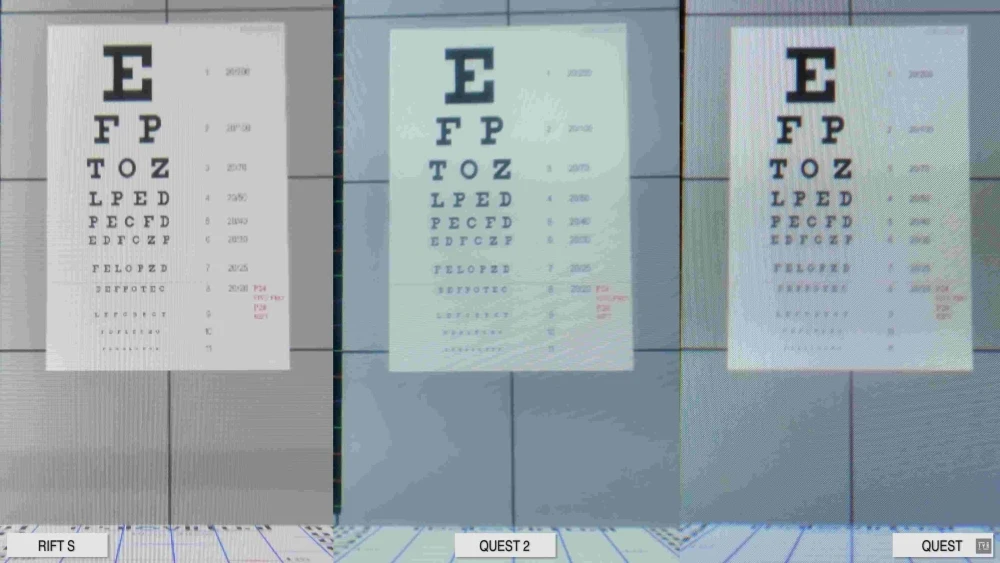

Solution in Quest 2 is much better than the original Quest. Rough graininess in the picture almost entirely disappears. | Image: Reddit
Comparison video and images of this kind in no way replace the real view through virtual reality glasses. Therefore, the cost to independently test and conclude which of them offer the best picture.

